Course scheduling with CSP
Project design
The objective of this project is to help students design and simulate their course schedules based on given the dataset of the course listing.
The course scheduler is considered as a constraint satisfaction problem by checking schedule conflicts and requirements to generate a feasible schedule with minimizing unsatisfied preference. We have assumed that every student must enroll as a full-time student, and they have a maximum credit limit. Each course contains information about time, prerequisites, instructor, and more. Each student has a profile of courses they took, degree requirements, level of degree, and more.
Data collection
We used CSC graduate and undergraduate course schedules for Fall 2022 taken from the ‘Class Search’ page provided by the university. The list of courses displays the course code, title, prerequisites or corequisites, available slots, day and time, section number of each section, instructor, and some other minor information.
Problem formulating
We formulated our problem in 4 main factors: Variable, Domains, Goal and Constraints.
Variables: All possible courses based on a student profile
Domains: “Taken” or “Not taken”
Initially, we checked some ways to set domains as courses and variables as “Day” or “Time”. But it is too complicated to assign values in this case. If the variables are regarded as “Day”, there are many cases to assign two or more values in one variable(e.g. Take two or more courses in the same day). Also, if the variables are “Time”, It is hard to handle it as “Time” is a continuous variable. Thus, we select the variables as a course and set the strategy to reduce the variables if the domain of a specific variable is “Not taken”.
Goal: In the courses’ combinations which are satisfying all hard constraints, finding optimal solutions which can satisfy as many soft constraints as possible.
Constraints: The constraints are divided into two parts: Hard constraint and Soft constraint. A hard constraint is the one that must be satisfied at all times. Soft constraints are good to satisfy as many as possible for optimal solutions. As our problem is in a real-world environment, there would be more constraints. However, we consider the constraints which can be derived from our dataset. It could be reasonable because we can considerably reduce the possible class schedule options following below constraints.
Hard constraints
The optimal solution must meet the following constraints.
- Course availability
- Course cannot be enrolled if it is full.
- Previous taken courses
- Students cannot take courses which they took in the previous semester.
- Degree/Track/Affiliation of students
- Students must register courses that fit their enrolled degree program. For example, master’s students cannot enroll in undergraduate low level classes, there are limitations to take courses provided from other departments.
- Upper level students cannot take lower level courses, and vice versa.
- Time conflicts
- It should prevent registering more than one course happening simultaneously
- Credit limitation
- Based on the minimum / maximum credits designated by CSC department, the summation of credits of courses taken by students should be in between minimum and maximum credits.
- Laboratory attendance
- Students must take one of the laboratory courses if the courses require it.
- Taking same courses
- It is not possible to take two or more courses which are in the same course code.
Courses 216 and 217 are the only exception that the lecture and laboratory sessions are separated. We assumed that 217 is the part of 216 and changed course number from 217 to 216 because students must take both courses to meet the course requirements.
Soft constraints
Soft constraints are not mandatory to meet, therefore, we calculated weight for each soft constraint. However, solutions generated after applying hard constraints are too many, so we decided to give a huge penalty if it does not meet soft constraints.
- Each degree level has minimum and maximum course numbers (assumption).
- Students with high-level standing cannot take lower level courses.
- Freshman/Sophomore: 100~300
- Junior: 200~500
- Senior: 300~500
- Masters/Doctorate: 500~900
- Course preference (count_matching)
- Students may have a list of courses that they want to take or not. The intersection between a given list and the generated solution contains at least 1 common course, we added the number of common courses to the weight.
- Each course preference is range -1(don’t want to take) to n(the number of courses that they want to take)
- Since the suggested output is large enough, we hugely deducted weight to reduce the number of optimal solutions if preference is a negative value. Otherwise, we added a given preference level of each course to the weight.
- Students must enroll at least the minimum credit hours, however, they can enroll more courses as long as it does not exceed maximum credit hours.
- The number of courses in the suggested solutions can vary depending on its weight.
- Students can enroll at most 3 credits for research courses.
- This is not mandatory.
- A student may want to enroll courses happening only on a particular day(s) (day_weight).
- This simple preference can be violated, courses scheduled on Friday can be enrolled depending on the situation.
- Preferences of each day(Monday to Friday) are given in the student’s profile as either 0 or 1 (e.g. M_0, T_1, W_1, TH_1, F_0). 1 means that a student is willing to take a course on a particular day, 0 means that a student does not prefer to have a class on a particular day.
- Since the suggested output is large enough, we hugely deducted weight to reduce the number of optimal solutions if a given value is a negative value.
Weight calculation
Weight functions are divided into two parts, which are ‘count_matching’ and ‘day_weight’. We think enrolling courses that students want should be more weighted than their day preferences. Therefore, the final weight is calculated with the following formula:
final_weight = 0.6*count_matching + 0.4*day_weight
Approach
Workflow overview
- Data preprocessing
- Generating list of possible courses based on student profile and unary hard constraints
- Searching solutions which satisfy all other binary/high-order hard constraints
- Finding optimal solution which satisfy maximum number of satisfied soft constraints
Generating list of possible courses
For generating possible courses to each student, we formulate a student profile. Student profile contains information such as degree, min/max credit, previous taken courses, courses which they prefer to take. With this profile and unary hard constraints (Course availability, Previous taken courses, Degree of students), we filtered possible courses which can fit a specific student. For example, If a degree of student is “undergraduate” and previous taken courses of the student is “111, 113, 216, 217”, the output is a list of courses without “Courses with no seat” and “Graduate level courses” and “course code 111, 113, 216, 217”.
Searching solutions satisfying other hard constraints
The basic algorithm is similar to the backtracking algorithm. For improving the efficiency of Backtracking search, we use Forwardchecking. In the dataset, there are courses requiring participation in the laboratory(almost in undergraduate courses). For this, in the Backtracking search, we divided the cases in two parts: the course with lecture and laboratory or the course with only lecture. In the former case, one of the laboratory courses is also added in “assignment” and Forwardchecking is executed given that “assignment”.
In the procedure, there are two points to be explained. First of all, in Forwardchecking, we concentrated on reducing variables not values. As we know, Forwardchecking is a methodology which uses constraints to reduce the options of values per each variable. In problem formulation, we set the domain as “Taken” or “Not taken”. If the variable of value is “Not taken” given a specific “assignment”, we no longer need to consider this variable until the result is “failure”. Thus, we just remove the variable in that “assignment”. Second, if a specific variable is searched, the variable is no longer considered in the same depth search. This is related to the characteristics that backtracking search is DFS. For example, let’s assume that possible courses given a specific assignment are [A, B, C]. If lecture “A” is searched, the algorithm will find all possible course lists satisfying hard constraints. Then at the time when lecture “B” is searched, there would be redundancy if lecture “A” is also contained in the possible courses as we already searched when lecture “A” is taken. By applying this strategy, we reduced the time taken to find all possible cases satisfying hard constraints.
Finding optimal solution which satisfy maximum number of satisfied soft constraints
Out of solutions that are generated after checking hard constraints and weighting soft constraints, we filtered top 5 solutions out of entire outputs ordered by weights in descent.
Results
| Student profile | Output |
|---|---|
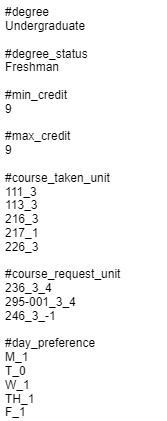 |
 |
| ↑ Student1’s profile | ↑ 14 solutions of student1’s profile. Highlighted solutions are with top 5 weights. PDF files are generated for those solutions. |
Visualized solution - example

Limitations and conclusion
Constraint satisfaction problem and its algorithms are applied in many real-world applications. We used a forward checking algorithm and backtracking to filter out hard constraints, however, its efficiency is relatively low when the maximum credit is getting larger. While working on this project, we got the course information and availability from the school website. However, due to our algorithm, our scraped data does not reflect real-time status. Courses listed in our solution may be already closed in reality. The last updated version is as of April 14, 2022. Also, some assumptions(No consideration of requisites and location of courses) we initially made are needed to be handled. For example, we initially tried to take care of the course’s prerequisites and corequisites. However, we decided to ignore these constraints because some prerequisites are not limited to computer science courses and the list of the courses taken in the student’s profile does not contain all courses offered outside computer science while some courses can actually require students to meet this requirements. In our future work, we take these assumptions into constraints to make a more optimal and practical course schedule.
Reference
[1] Jwodder. “Jwodder/Schedule: Weekly Schedule Typesetter.” GitHub, github.com/jwodder/schedule.